Построения с помощью циркуля и линейки - раздел евклидовой геометрии, известный с античных времён. задачах на построение циркуль и линейка считаются идеальными инструментами, в частности:

• Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
• Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).

• 1 Пример
• 2 Формальное определение
• 3 Известные задачи
  • 3.1 Построение правильных многоугольников
  • 3.2 Неразрешимые задачи
• 4 Возможные и невозможные построения
• 5 Вариации и обобщения
• 6 Интересные факты
• 7 См. также
• 8 Примечания
• 9 Литература

Пример

Разбиение отрезка пополам

Задача на бисекцию . С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружности с центром в точках A и B радиусом AB.
• Находим точки пересечения P и Q двух построенных окружностей (дуг).
• По линейке проводим отрезок или линию, проходящую через точки P и Q.
• Находим искомую середину отрезка AB - точку пересечения AB и PQ.

Формальное определение

В задачах на построение рассматриваются множество всех точек плоскости, множество всех прямых плоскости и множество всех окружностей плоскости, над которыми допускаются следующие операции:

1. Выделить точку из множества всех точек:
   1. произвольную точку
   2. произвольную точку на заданной прямой
   3. произвольную точку на заданной окружности
   4. точку пересечения двух заданных прямых
   5. точки пересечения/касания заданной прямой и заданной окружности
   6. точки пересечения/касания двух заданных окружностей
2. «С помощью линейки » выделить прямую из множества всех прямых:
   1. произвольную прямую
   2. произвольную прямую, проходящую через заданную точку
   3. прямую, проходящую через две заданных точки
3. «С помощью циркуля » выделить окружность из множества всех окружностей:
   1. произвольную окружность
   2. произвольную окружность с центром в заданной точке
   3. произвольную окружность с радиусом, равным расстоянию между двумя заданными точками
   4. окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками

В условиях задачи задается некоторое множество точек. Требуется с помощью конечного количества операций из числа перечисленных выше допустимых операций построить другое множество точек, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

1. Описание способа построения заданного множества.
2. Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
3. Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Известные задачи

• Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
• Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Построение правильных многоугольников

Основная статья: Теорема Гаусса - Ванцеля Построение правильного пятиугольника

Античным геометрам были известны способы построения правильных n-угольников для, и.

В 1796 году Гаусс показал возможность построения правильных n-угольников при, где - различные простые числа Ферма. 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

• Трисекция угла - разбить произвольный угол на три равные части.
• Удвоение куба - построить ребро куба вдвое большего по объёму, чем данный куб
• Квадратура круга - построить квадрат, равный по площади данному кругу.

Лишь в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

• Другая известная неразрешимая с помощью циркуля и линейки задача - построение треугольника по трём заданным длинам биссектрис. Причём эта задача остаётся неразрешимой даже при наличии трисектора.

Возможные и невозможные построения

Каждое построение на самом деле является решением какого-либо уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа - графического решения уравнения определенного типа. рамках вышеописанных требований возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений квадратных уравнений.

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного корня из исходных чисел (длин отрезков). Например,

• Если задан только отрезок длины, то невозможно представить в таком виде (отсюда невозможность удвоения куба).
• Возможность построить правильный 17-угольник следует из выражения на косинус угла:

Вариации и обобщения

• Построения с помощью одного циркуля. По теореме Мора - Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
• Построения с помощью одной линейки. Легко заметить, что с помощью одной линейки можно проводить только проективно-инвариантные построения. частности,
  • невозможно даже разбить отрезок на две равные части,
  • также невозможно найти центр данной окружности.

Однако

• • при наличии на плоскости заранее проведённой окружности с отмеченным центром с одной линейкой можно провести те же построения, что и циркулем и линейкой (Теорема Штейнера - Понселе).
  • Если на линейке есть две засечки, то построения с помощью неё эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон).
• Построения с помощью инструментов с ограниченными возможностями. задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу.
• Построения с помощью плоского оригами. см. правила Худзита

• Узор на флаге Ирана описывается как построение с помощью циркуля и линейки.

См. также

• Программы динамической геометрии позволяют выполнять построения с помощью циркуля и линейки на компьютере.

Примечания

1. Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
2. Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
3. Стандарт флага Ирана (перс.)

Литература

• А. Адлер. Теория геометрических построений / Перевод с немецкого Г. М. Фихтенгольца. - Издание третье. - Л.: Учпедгиз, 1940. - 232 с.
• И. И. Александров. Сборник геометрических задач на построение. - Издание восемнадцатое. - М.: Учпедгиз, 1950. - 176 с.
• Б. И. Аргунов, М. Б. Балк. Геометрические построения на плоскости. Пособие для студентов педагогических институтов. - Издание второе. - М.: Учпедгиз, 1957. - 268 с.
• А. М. Воронец. Геометрия циркуля. - М.-Л.: ОНТИ, 1934. - 40 с. - (Популярная библиотека по математике под общей редакцией Л. А. Люстерника).
• В. А. Гейлер Неразрешимые задачи на построение // СОЖ. - 1999. - № 12. - С. 115-118.
• В. А. Кириченко Построения циркулем и линейкой и теория Галуа // Летняя школа «Современная математика». - Дубна, 2005.
• Ю. И. Манин. Книга IV. Геометрия // Энциклопедия элементарной математики. - М.: Физматгиз, 1963. - 568 с.
• Ю. Петерсен. Методы и теории решения геометрических задач на построение. - М.: Типография Э. Лисснера и Ю. Романа, 1892. - 114 с.
• В. В. Прасолов. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. - М.: Наука, 1992. - 80 с. - (Популярные лекции по математике).
• Я. Штейнер. Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга. - М.: Учпедгиз, 1939. - 80 с.
• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. - М.: Просвещение, 1991. - С. 80. - 383 с. - ISBN 5-09-001287-3.

Построение с помощью циркуля и линейки Информацию О

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Учебник: Геометрия, 7-9: учебник для общеобразовательных учреждений / (Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.) – 16 изд. – М.: Просвещение, 2011.

Цели урока:

1. дать представление о новом классе задач на построение;
2. рассмотреть наиболее простые задачи на построение;
3. научить учащихся решать такие задачи.

Задачи:

Образовательный аспект:

• дать представление о новом классе задач – построение геометрических с помощью циркуля и линейки без масштабных делений;
• формировать практические умения работы;
• расширить знания об истории геометрии.

Развивающий аспект:

• развитие навыков самоконтроля;
• формирование ИКТ – компетентности;
• формирование логического мышления.

Воспитательный аспект:

• воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при изучении темы;
• воспитание интереса к истории математики, как науки.

Тип урока: комбинированный.

Формы организации учебной деятельности: индивидуальная, коллективная.

Этапы урока:

• подготовка к активной учебной деятельности;
• применение знаний;
• подведение итогов и рефлексия;
• информация о домашнем задании.

Оборудование:

• Учебное пособие, тетрадь, карандаш, авторучка, линейка, циркуль, раздаточный материал (КИМ);
• Компьютер, с минимальными техническими требованиями: Windows 95/98/ME/NT/2000/XP, 7.
• Муьтимедийный проектор, экран.

Ресурсы урока:

• тестовые задания (КИМ) приложение 1 ;
• презентация;
• оценка степени усвоения материала приложение 3 .

План урока:

№	Этап урока	Цель урока	Время
1.	Организационный момент(слайды 1-2)	Сообщение темы урока;Постановка цели урока;Сообщение этапов урока.	2 мин.
2.	Повторение. Проверка домашнего задания.(слайд 3)	Проверка теоретических знаний учащихся по теме окружность при выполнении теста.	5 мин.
3.	Подготовка учащихся к восприятию нового материала.(слайды 4-8)	Актуализация опорных знаний	10 мин.
4.	Изучение нового материала(слайды 9-19)	Отработка навыков решения простейших задач на построение циркулем и линейкой, рассмотренных в учебнике.	25 мин.
5.	Итог урока.	Подведение итогов урока.	2 мин.
6.	Домашнее задание.(слайд 20)	Инструктаж по домашнему заданию.	1 мин.

ХОД УРОКА

1. Организационный момент:

Тема сегодняшнего урока - «Примеры задач на построение» (слайд 1).

Цель урока – рассмотреть наиболее простые задачи на построение, которые решаются только с помощью циркуля и линейки без делений; научиться решать их (слайд 2).

2. Повторение. Проверка домашнего задания:

Мы с вами изучили тему « Окружность» и сегодня проверим с помощью теста ваши знания. Выполнить задание теста (каждому раздаются КИМы с тестовым заданием). Для каждого вопроса выберите правильный вариант ответа. Самостоятельно оцените свои знания, подсчитав количество верных ответов. Если верных ответов 6 - оценка «5», если верных ответов 5 – оценка «4», если верных ответов 4 – оценка «3», меньшее количество верных ответов – оценка « 2».

(Верные ответы на слайде 3 презентации).

3. Подготовка учащихся к восприятию нового материала:

Вводная беседа учителя:

Мы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, чертили углы, треугольники и другие фигуры с помощью различных инструментов. При построении отрезка заданной длины использовалась линейка с миллиметровыми делениями, а при построении угла заданной градусной меры – транспортир.

В домашней работе у вас была такая задача:

Начертите треугольник АВС такой, что АВ = 3,6 см, АС = 2,7 см, А = 48°. Какие инст рументы вы использовали для решения этой задачи?

Итак, мы использовали линейку с миллиметровыми делениями и транспортир. Но есть такие задачи, в которых бывает оговорено, с помощью каких инструментов нужно построить предлагаемую геометрическую фигуру (слайд 4-5).

Задача 1. С помощью циркуля и линейки без делений на данном луче от его начала отложить отрезок, равный данному. Чертёж на экране.

(Учащиеся предлагают варианты решений).

А теперь проверим ваше решение (см. слайд 6)

Таким образом, многие построения в геометрии могут быть выполнены с помощью только циркуля и линейки без делений (слайд 7).

В дальнейшем, говоря о задачах на построение, мы будем иметь в виду именно такие построения.

Задачи на построение циркулем и линейкой являются традиционным материалом, изучаемым в курсе планиметрии. Обычно эти задачи решаются по схеме, состоящей из четырех частей (посмотреть с. 95–96 учебника). Сначала рисуют (чертят) искомую фигуру и устанавливают связи между данными задачи и искомыми элементами. Эта часть решения называется анализом . Она дает возможность составить план решения задачи.

Затем по намеченному плану выполняется построение циркулем и линейкой.

После этого нужно доказать , что построенная фигура удовлетворяет условиям задачи.

И наконец, необходимо исследовать , при любых ли данных задача имеет решение, и если имеет, то сколько решений.

В тех случаях, когда задача достаточно простая, отдельные части, например анализ или исследование, можно опустить (слайд 8).

В VII классе мы решим простейшие задачи на построение циркулем и линейкой, в других классах будем решать более сложные задачи.

4. Изучение нового материала:

И так, наша задача – выполнить задачи на построение только с помощью двух инструментов: циркуля и линейки без масштабных делений.

Что можно делать с их помощью? Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки. С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку (слайд 9).

Выполняя эти несложные операции, мы сможем решить много интересных задач на построение (слайд 10):

1. На данном луче от его начала отложить отрезок, равный данному.
2. Отложить от данного луча угол, равный данному.
3. Построить биссектрису данного неразвернутого угла.
4. Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
5. Построить середину данного отрезка.

Мы уже решили задачу № 1.

Теперь с помощью компьютера рассмотрим решение задачи № 2. Выполняйте соответствующие построения в тетради (слайды 11-12).

А теперь рассмотрим задачи № 3 – 5 (слайд 13-18).

(выполняются соответствующие построения и описания задач в тетради)

После выполнения работы, учитель обращает внимание учащихся на то, что такие задачи рассматривались в древности (слайд 19).

А теперь обратимся к истории геометрии. Древнегреческие математики достигли чрезвычайно большого искусства в геометрических построениях с помощью циркуля и линейки. Они доказали, что угол можно разделить и на четыре равных угла. Для этого нужно разделить его пополам, а затем построить биссектрису каждой половинки. А можно ли с помощью циркуля и линейки разделить угол на три равные части? Эта задача, получившая название задачи о трисекции угла, в течение многих веков привлекала внимание математиков. Однако она не поддавались их усилиям. Лишь в прошлом веке было доказано, что для произвольного угла такое построение невозможно.

Есть и другие задачи на построение, про которые известно, что они неразрешимы с помощью циркуля и линейки. Я предлагаю вам самостоятельно найти материал, содержащий информацию для ознакомления с этими задачами.

5. Подведение итогов урока:

Мы изучили много нового, узнали какие задачи можно решить только с помощью циркуля и линейки. У вас у каждого лежит лист с вопросами. Оцените свою работу на сегодняшнем уроке, выбрав один из предложенных вариантов ответа.

1. Оцените степень сложности урока. Вам было на уроке:
   • легко;
   • обычно;
   • трудно
2. Оцените степень вашего усвоения материала:
   • усвоил полностью, могу применить;
   • усвоил полностью, но затрудняюсь в применении;
   • усвоил частично;
   • не усвоил.

Собрать листочки для оценки степени усвоения материала сегодняшнего урока, чтобы на следующем уроке правильно организовать работу. Сообщаются оценки за урок, включая оценки за тест по теме « Окружность».

6. Домашнее задание:

• ответить на вопросы 17–21 на стр. 50;
• решить задачи №№ 153, 154 (слайд 20).

2. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен
:
количество сторон (в нашем случае 8.
Получаем точки А1, А2
, A3, A4, A5, A6, A7, A8.

А2
А1
А8
А7
А6
А5
А4
А3
n-
угольника
3. Соединим центры окружности и одну из точек их пересечения

Мы получаем правильный треугольник

1
. Построим 2 окружности проходящие через центр друг друга.

2
. Соединим центры прямой, получив одну из сторон пятиугольника.

3. Соединим точки пересечения окружностей.

5 . Соединяем точки пересечения всех прямых с исходной окружностью.

Мы получаем правильный шестиугольник
Доказательство существования правильного
n-
угольника
Если
n
(число углов многоугольника) больше 2, то такой многоугольник существует.
Пробуем построить 8ми угольник и докажем это.
1. Возьмем окружность произвольного радиуса с центром в точке « О »

Построение треугольника при помощи циркуля и линейки
«
O
» .

2. Построим еще одну окружность того же радиуса проходящая через точку «О».

4. Соединим точки, лежащие на окружности.

Получаем правильный восьмиугольник.
Построение правильных многоугольников с помощью циркуля и линейки.

В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных
n-
угольников, если равенство
n =
+ 1
, где
n –
количество углов, а
k
– любое натуральное число
.
Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, равных частей
.
В 1836 году
Ванцель
доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя.

Построение правильного шестиугольника при помощи циркуля и линейки.

4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью

ЛИТЕРАТУРА
Атанасян
Л. С. и др. Геометрия: Учебник для 7-9 классов образовательных учреждений. – М: «Просвещение». 1998.
Б. И. Аргунов, М. Б.
Балк
. Геометрические построения на плоскости, Пособие для студентов педагогических институтов. Издание второе. М.,
Учпедгиз
, 1957 – 268 с.
И. Ф.
Шарыгин
, Л. Н.
Ерганжиева
. «Наглядная геометрия».
Еще
одним
великим математиком изучавшим правильные многоугольники был
Евклид
или
Эвклид
(др. греч.
Εὐκλείδης
, от «добрая слава»
ок
. 300 г. до н. э.)
–
автор первого из дошедших до нас теоретических трактатов по математике
.
Его главная работа «Начала» содержит изложение планиметрии, стереометрии и ряды вопросов теории чисел
;
в ней он подвёл итог дальнейшего развития математики. В
IV
книге он описал построение правильных многоугольников при
n
равном
3
, 4, 5, 6, 15

и определил первый критерий построения многоугольников.
Построение правильного восьмиугольника.
1. Построим восьмиугольник при помощи четырехугольника.
2. Соединим противоположные вершины четырёхугольника
3. Проведем биссектрисы углов образованных пересекающимися диагоналями

Треугольники
, сторонами которых являются ближайшие радиусы и
стороны получившегося восьмиугольника равны по двум сторонам и углу между ними, соответственно стороны восьмиугольника равны и он является правильным. Данное доказательство применимо не только к восьмиугольникам
,
но и к многоугольникам с количеством углов
больше 2-х
. Что и требовалось доказать
.
Доказательство существования правильного
n-
угольника

А2
А1
А8
А7
А6
А5
А4
А3

4 . Проводим прямые через точки пересечения окружностей
5. Соединяем точки пересечения прямых и окружности

Получаем правильный четырёхугольник.
Построение правильного пятиугольника методом Дюрера.
6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника.
7. Достроим до пятиугольника

Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одним из них был
Архимед.
Архимед
– известный древнегреческий математик, физик и инженер. Он сделал множество открытий в геометрии, ввёл основы механики, гидростатики, создал множество важных изобретении. Архимед был просто одержим математикой. Он забывал о пище, совершенно не заботился о себе. Его открытия послужили для современных изобретений.
Построение правильного шестиугольника при помощи циркуля и линейки.

1. Построим окружность с центром в точке
O
.
2. Проведем прямую линию через центр окружности.
3. Проведем дугу окружность того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.

Презентация на тему: «Построение правильных многоугольников с помощью циркуля и линейки»
Подготовил:
Гурома
Денис
ученик 10 класса МБОУ школы №3
Учитель:
Наимова
Татьяна Михайловна
2015 год
3. Поочередно соединяем их и получаем правильный восьмиугольник.
Доказательство существования правильного
n-
угольника

А2
А1
А8
А7
А6
А5
А4
А3
Построение правильного четырёхугольника.

1. Построим окружность с центром в точке
O
.
2. Проведем 2 взаимно перпендикулярные диаметра.
3. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).

Построение правильного пятиугольника методом Дюрера.

4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей.

5. Проведем 2 отрезка.

Геометрические задачи на построение

С помощью циркуля и линейки

учащаяся 8-А класса

Руководитель: Москаева В.Н.,

учитель математики

Нижний Новгород

Введение

Наглядность, воображение принадлежат больше искусству, строгая логика – привилегия науки. Сухость точного вывода и живость наглядной картины – «лёд и пламень не столь различны меж собой». Геометрия соединяет в себе эти две противоположности.

А. Д. Александров

Собираясь в школу, мы не забываем положить в портфель циркуль, линейку и транспортир. Эти инструменты помогают выполнить грамотно чертежи и красиво нарисовать. Данные инструменты используют инженеры, архитекторы, рабочие, конструкторы одежды, обуви, строители, ландшафтные дизайнеры. Хотя существуют компьютеры, но на стройке, в саду их пока не используешь.

Машина рисует мгновенно в течение нескольких секунд. Математик должен потратить довольно много времени, чтобы на языке, понятном машине объяснить ей то, что она должна сделать - написать программу и ввести её в машину, поэтому конструкторы нередко предпочитают работать с простейшими и древнейшими инструментами – циркулем и линейкой.

Что может быть проще? Гладкая дощечка с ровным краем - линейка, две заостренные палочки, связанные на одном конце - циркуль. С помощью линейки через две заданные точки проводят прямую. С помощью циркуля проводят окружности с данным центром и данного радиуса, отложить отрезок, равный данному.

Циркуль и линейка известны более 3 тысячи лет были уже известны, 200-300 лет назад их украшали орнаментами и узорами. Но, несмотря на это они и сейчас исправно служат нам. Простейших инструментов достаточно для огромного количества построений. Древние греки думали, что возможно любое разумное построение выполнить этими инструментами, пока не обнаружили три знаменательные задачи древности: «квадратуру круга», «трисекцию угла», «удвоение куба».

Поэтому считаю тему моей работы современной и важной для деятельности человека во многих сферах деятельности человека.

Все прекрасно знают, что математика используется в самых разных профессиях и жизненных ситуациях. Математика – предмет непростой. И геометрию большинство учащихся называет «трудной». Задачи на построение отличаются от традиционных геометрических задач.

Решение задач на построение развивает геометрическое мышление гораздо полнее и острее, чем решение задач на вычисление, и способно вызвать увлечение работой, которое приводит к усилению любознательности и к желанию расширить и углубить изучение геометрии.

Несмотря на богатое историческое прошлое, проблема решения задач на построение остается актуальной и в 21-м веке. В наше время бурно развиваются компьютерные технологии с применением графических редакторов для рисования геометрических объектов. Средства создания геометрических объектов изменились в связи с появлением новых компьютерных технологий. Однако, как и в глубокой древности, основными элементами при построении геометрических объектов остаются окружность и прямая, другими словами циркуль и линейка. С появлением новых компьютерных технологий возникли новые проблемы построения с использованием тех же объектов - прямой и окружности. Вот почему проблема решения задач на построение становится ещё более актуальной.

Программа по геометрии предполагает изучение лишь простейших приемов и методов построений. Но применение этих приемов часто вызывает затруднения. Поэтому, объектом моего исследования являются геометрические фигуры, построенные с помощью циркуля и линейки.

Цель моей работы: рассмотреть различные способы построения геометрических фигур с помощью циркуля и линейки.

Методы исследования:

ü Анализ уже существующих способов построений

ü Поиск новых способов, простых в применении (ГМТ и построения Штейнера)

Задачи:

ü получить более полное представление о различных способах построений

ü проследить за развитием этого фрагмента геометрии в истории математики

ü продолжить развитие исследовательских умений.

Из истории геометрического построения циркулем и линейкой.

Традиционное ограничение орудий геометрических построений восходит к глубокой древности. В своей книге "Начала" Евклид (III век до н. э.) строго придерживается геометрических построений, выполняемых циркулем и линейкой, хотя названий инструментов он нигде не упоминает. Ограничения, по-видимому, были связаны с тем, что эти инструменты заменили собой веревку, первоначально служившую как для проведения прямых, так и для описания окружностей. Но многие историки-математики объясняют произведенный Евклидом отбор материала тем, что он, следуя Платону и пифагорейцам, считал только прямую и круг "совершенными" линиями.

Искусство построения геометрических фигур было в высокой степени развито в Древней Греции. Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем – линейки и двух заостренных палок, связанных на одном конце – циркуля. Однако этих простейших инструментов оказалось достаточно для выполнения огромного множества различных построений. Древним грекам даже казалось, что любое разумное построение можно совершить этими инструментами, пока они не столкнулись с тремя знаменитыми впоследствии задачами.

Они издавна преобразовывали любую прямолинейную фигуру с помощью циркуля и линейки в произвольную прямолинейную фигуру, равновеликую ей. В частности, всякая прямолинейная фигура преобразовывалась в равновеликий ей квадрат. Поэтому понятно, что появилась мысль обобщить эту задачу: построить с помощью циркуля и линейки такой квадрат, площадь которого была бы равна площади данного круга. Это задача получила название квадратуры круга. Следы этой задачи можно усмотреть еще в древнегреческих и вавилонских памятниках второго тысячелетия до н.э. Однако ее непосредственная постановка встречается в греческих сочинениях V века до н.э.

Еще две задачи древности привлекали внимание выдающихся ученых на протяжении многих веков. Это задача об удвоении куба. Она состоит в построении циркулем и линейкой куба, имеющего объем вдвое больший, чем объем данного куба. Ее появление связывают с легендой, что на острове Делос в Эгейском море оракул, чтобы избавить жителей от эпидемии чумы, повелел удвоить алтарь, имевший форму куба. И третья задача трисекции угла о делении угла на три равные части с помощью циркуля и линейки .

Эти три задачи, так называемые 3 знаменитые классические задачи древности, привлекали внимание выдающихся математиков на протяжении двух тысячелетий. И лишь в середине XIX века была доказана их неразрешимость, то есть невозможность указанных построений лишь с использованием только циркуля и линейки. В математике это были первые результаты о неразрешимости задач, когда средства решения указаны. Они были получены средствами не геометрии, а алгебры (с помощью перевода этих задач на язык уравнений), что еще раз подчеркнуло единство математики. Не поддаваясь решению, эти проблемы обогатили математику значительными результатами, привели к созданию новых направлений математической мысли.

Еще одной интереснейшей задачей на построение с помощью циркуля и линейки является задача построения правильного многоугольника с заданным числом сторон. Древние греки умели строить правильный треугольник, квадрат, правильные пятиугольник и 15-угольник, а также все многоугольники, которые получаются из них путем удвоения сторон, и только их. Лишь в 1796 году великий немецкий математик К.Ф.Гаусс открыл способ построения правильного 17-угольника при помощи циркуля и линейки и указал все значения N, при которых возможно построение правильного N-угольника указанными средствами. Первокурсник Геттингенского университета Карл Гаусс решил задачу, перед которой математическая наука пасовала более 2 с лишним тысяч лет. Таким образом, была доказана невозможность построения с помощью циркуля и линейки правильных 7, 9, 11, 13, 18, 21, 22, 23 и т.д. угольников.

Теория построения при помощи циркуля и линейки получила свое дальнейшее развитие. Был получен ответ на вопрос: можно ли решить задачу с помощью только одного из двух рассматриваемых инструментов, и достаточно неожиданный. Независимо друг от друга, датчанин Г.Мор в 1672 году и итальянец Л.Маскерони в 1797 году доказали, что любая задача на построение, разрешаемая циркулем и линейкой, может быть точно решена с помощью только одного циркуля. Это кажется невероятным, но это так. А в XIX веке было доказано, что любое построение, выполняемое с помощью циркуля и линейки можно провести лишь с помощью одной линейки, при условии, что в плоскости построения задана некоторая окружность и указан ее центр.

3. Простейшие задачи на построение геометрических фигур с помощью циркуля и линейки

Рассмотрим основные (элементарные) построения, которые наиболее часто встречаются в практике решения задач на построение. Задачи такого рода рассматриваются уже в первых главах школьного курса.

Построение 1. Построение отрезка, равного данному.

Дано: отрезок длины а.

Построить: отрезок АВ длины а.

Построение:

Построение 2. Построение угла, равного данному.

Дано: ∟AOB.

Построить: ∟ KMN, равный ∟ АОВ.

Построение:

Построение 3. Деление отрезка пополам (построение середины отрезка).

Дано: отрезок АВ.

Построить: точку О – середину АВ.

Построение:

Построение 4. Деление угла пополам (построение биссектрисы угла).

Дано: ∟ АВС.

Построить: ВD – биссектрису ∟АВС.

Построение:

Построение 5. Построение перпендикуляра к данной прямой, проходящей через данную точку.

а) Дано: прямая а, точка A а.

Построить:

прямой а.

Построение :

б) Дано: прямая а, точка A a.

Построить: прямую, проходящую через точку А, перпендикулярно к

прямой а.

Построение:

Построение 6 . Построение прямой, параллельной данной прямой и проходящей через данную точку.

Дано: прямая а, точка A a.

Построить: прямую, проходящую через точку А, параллельно прямой а.

I способ (через два перпендикуляра).

Построение:

II способ (через параллелограмм).

Построение:

Построение 7. Построение треугольника по трем сторонам.

Дано: отрезки длины a, b, c.

Построить: Δ ABC.

Построение:

Построение 8. Построение треугольника по двум сторонам и углу между ними.

Дано: отрезки длины b, c, угол α.

Построить: треугольник ABC.

Построение:

Построение 9. Построение треугольника по стороне и двум прилежащим углам.

Дано: отрезок длины c, углы α и β.

Построить: ΔABC.

Построение:

Построение 10. Построение касательной к данной окружности, проходящей через данную точку.

Дано: окружность (О), точка А вне ее.

Построить: касательную к окружности ω(О), проходящую через точку А.

Построение:

Рассмотренные задачи входят в качестве составных частей в решение более сложных задач, поэтому в дальнейшем, этапы основных построений не описываются.

Решение задач на построение состоит из четырех частей:

1. Предположив, что задача решена, делаем от руки приблизительный чертеж искомой фигуры и затем, внимательно рассматриваем начерченную фигуру, стремясь найти такие зависимости между данными задачи и искомыми, которые позволили бы свести задачу на другие, известные ранее. Эта самая важная часть решения задачи, имеющая целью составить план решения, носит название анализа.

2. Когда таким образом план решения найден, выполняют сообразно ему построение.

3. Доказательство - для проверки правильности плана на основании известных теорем доказывают, что полученная фигура удовлетворяет всем требованиям задачи.

4. Исследование - задаются двумя вопросами:

1) При всяких ли данных возможно решение?

2) Сколько существует решений?

Рассмотрим применение данных этапов на примере решения следующей задачи.

Задача: Построить треугольник, зная его основание b, угол A, прилежащий к основанию, и сумму s двух боковых сторон.

Анализ: Предположим, что задача решена, т.е. найден такой ΔAВС, у которого основание AС=b, ∟ВАС=A и AВ+ВС=s . Рассмотрим теперь полученный чертеж. Сторону AС, равную b , ∟ВАС=A , мы строить умеем. Значит, остается найти на другой стороне ∟A такую точку В , чтобы сумма AВ+ВС равнялась s . Продолжив AВ , отложим отрезок AD , равный s . Теперь вопрос приводится к тому, чтобы на прямой AD отыскать такую точку В , которая была бы одинаково удалена от С и D . Такая точка как мы знаем, должна лежать на перпендикуляре, проведенном к отрезку СD через его середину. Точка В найдется в пересечении этого перпендикуляра с АD .

Построение:

1. Строим ∟А , равный данному углу

2. На его сторонах откладываем AС=b и AD=s

3. Через середину отрезка прямой СD проводим перпендикуляр ВЕ

4. ВЕ пересекает AD в точке В

5. Соединяем точки В и С

6. ΔAВС - искомый.

Доказательство:

Рассмотрим полученный ΔAВС, в нем ∟А равен данному углу (по пункту №1 построения). Сторона AС=b (пункт №2) и стороны АВ и ВС в сумме составляют s (пункты №2,3,4). Следовательно по 1-му признаку равенства треугольников ΔAВС - искомый.

Исследование:

1. При всяких ли данных возможно решение?

Рассматривая построение, мы замечаем, что задача возможна не при всяких данных. Действительно, если сумма s задана слишком малой сравнительно с b, то перпендикуляр ВЕ может не пересечь отрезка AD (или пересечет его продолжение за точку D), в этом случае задача окажется невозможной.

И, независимо от построения, можно видеть, задача невозможна, если s < b или s =b , потому что не может быть такого треугольника, у которого сумма двух сторон была бы меньше или равна третьей стороне.

2. Сколько существует решений?

В том случае, когда задача возможна, она имеет только одно решение, т.е. существует только один треугольник, удовлетворяющий требованиям задачи, так как пересечение перпендикуляра ВЕ с прямой AD может быть только в одной точке.

©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-04-27

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №34 с углубленным изучением отдельных предметов

МАН, физико-математическая секция

«Геометрические построения с помощью циркуля и линейки»

Выполнила: ученица 7 «А» класса

Батищева Виктория

Руководитель: Колтовская В.В.

Воронеж, 2013

3. Построение угла равного данному.

Проведем произвольную окружность с центром в вершине А данного угла (рис.3). Пусть В и С - точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О-начальной точке данной полупрямой. Точку пересечения этой окружности с данной полупрямой обозначим С 1 . Опишем окружность с центром С 1 и Рис.3

радиусом ВС. Точка В 1 пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.

6. Построение перпендикулярных прямых.

Проводим окружность с произвольным радиусом r с центром в точке O рис.6. Окружность пересекает прямую в точках A и B. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей. Точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

Искомая прямая проходит через точки С и О.

Рис.6

Известные задачи

1. Задача Брахмагупты

Построить вписанный четырехугольник по четырем его сторонам. Одно из решений использует окружность Аполлония. Решим задачу Аполлония, используя аналогию между трехокружником и треугольником. Как мы находим окружность, вписанную в треугольник: строим точку пересечения биссектрис, опускаем из нее перпендикуляры на стороны треугольника, основания перпендикуляров (точки пересечения перпендикуляра со стороной, на которую он опущен) и дают нам три точки, лежащие на искомой окружности. Проводим окружность через эти три точки – решение готово. Точно также мы поступим с задачей Аполлония.

2. Задача Аполлония

Построить с помощью циркуля и линейки окружность, касающуюся трех данных окружностей. По легенде, задача сформулирована Аполлонием Пергским примерно в 220 г. до н. э. в книге «Касания», которая была потеряна, но была восстановлена в 1600 г. Франсуа Виетом, «галльским Аполлонием», как его называли современники.

Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.

Построение правильных многоугольников.

П

равильный (или равносторонний ) треугольник - это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны правильного треугольника равны между собой, а все углы равны 60°. Чтобы построить равносторонний треугольник нужно разделить окружность на 3 равные части. Для этого необходимо провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.

Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения через деление окружности на 6 частей. Используем равенство сторон правильного шестиугольника радиусу описанной окружности. Из противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.

Построение правильного пятиугольника.

П
равильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.

Вот один из методов построения правильного пятиугольника в заданной окружности:

Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O . (Это зелёная окружность на схеме справа).

Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .

Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью, как точку B .

Постройте точку C посередине между O и B .

C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .

Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F .

Проведите окружность с центром в E через точку A G .

Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .

Постройте правильный пятиугольник AEGHF .

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

Трисекция угла - разбить произвольный угол на три равные части.

Иначе говоря, необходимо построить трисектрисы угла - лучи, делящие угол на три равные части. П. Л. Ванцель доказал в 1837 году, что задача разрешима только тогда, когда например, трисекция осуществима для углов α = 360°/n при условии, что целое число n не делится на 3. Тем не менее, в прессе время от времени публикуются (неверные) способы осуществления трисекции угла циркулем и линейкой.

Удвоение куба - классическая античная задача на построение циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба.

В современных обозначениях, задача сводится к решению уравнения . Всё сводится к проблеме построения отрезка длиной . П. Ванцель доказал в 1837 году, что эта задача не может быть решена с помощью циркуля и линейки.

Квадратура круга - задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу .

Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины π. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа π, которая была доказана в 1882 году Линдеманом.

Другая известная неразрешимая с помощью циркуля и линейки задача - построение треугольника по трём заданным длинам биссектрис .

Причём эта задача остаётся неразрешимой даже при наличии трисектора.

Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

А ЗНАЕТЕ ЛИ ВЫ, ЧТО...

(из истории геометрических построений)

Когда-то в построение правильных многоугольников вкладывали мистический смысл.

Так, пифагорейцы, последователи религиозно-философского учения, основанного Пифагором, и жившие в древней Греции (V I-I V вв. до н. э.), приняли в качестве знака своего союза звездчатый многоугольник, образованный диагоналями правильного пятиугольника.

Правила строгого геометрического построения некоторых правильных многоугольников изложены в книге «Начала» древнегреческого математика Евклида, жившего в III в. до н.э. Для выполнения этих построений Евклид предлагал пользоваться только линейкой и циркулем, который в то время был без шарнирного устройства соединения ножек (такое ограничение в инструментах было непреложным требованием античной математики).

Правильные многоугольники нашли широкое применение и в античной астрономии. Если Евклида построение этих фигур интересовало с точки зрения математики, то для древнегреческого астронома Клавдия Птолемея (около 90 - 160 г. н. э.) оно оказалось необходимым как вспомогательное средство при решении астрономических задач. Так, в 1-й книге «Альмагесты» вся десятая глава посвящена построению правильных пяти- и десятиугольников.

Однако помимо чисто научных трудов, построение правильных многоугольников было неотъемлемой частью книг для строителей, ремесленников, художников. Умение изображать эти фигуры издавна требовалось и в архитектуре, и в ювелирном деле, и в изобразительном искусстве.

В «Десяти книгах о зодчестве» римского архитектора Витрувия (жившего примерно в 63 -14 гг. до н. э.) говорится, что городские стены должны иметь в плане вид правильного многоугольника, а башни крепости «следует делать круглыми или многоугольными, ибо четырехугольник скорее разрушается осадными орудиями».

Планировка городов очень интересовала Витрувия, который считал, что нужно спланировать улицы так, чтобы вдоль них не дули основные ветры. Предполагалось, что таких ветров восемь и что они дуют в определенных направлениях.

В эпоху Возрождения построение правильных многоугольников, и в частности пятиугольника, представляло не простую математическую игру, а являлось необходимой предпосылкой для построения крепостей.

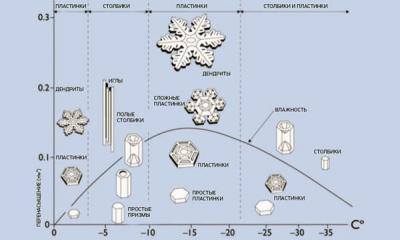
Правильный шестиугольник явился предметом специального исследования великого немецкого астронома и математика Иоганна Кеплера (1571-1630), о котором он рассказывает в своей книге «Новогодний подарок, или о шестиугольных снежинках». Рассуждал о причинах того, почему снежинки имеют шестиугольную форму, он отмечает, в частности, следующее: «...плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур правильный шестиугольник покрывает наибольшую площадь»

0дним из наиболее известных ученых, занимавшихся геометрическими построениями, был великий немецкий художник и математик Альбрехт Дюрер (1471 -1528), который посвятил им значительную часть своей книги «Руководства...». Он предложил правила построения правильных многоугольников с 3. 4, 5... 16-ю сторонами. Методы деления окружности, предложенные Дюрером, не универсальны, в каждом конкретном случае используется индивидуальный прием.

Дюрер применял методы построения правильных многоугольников в художественной практике, например, при создании разного рода орнаментов и узоров для паркета. Наброски таких узоров были сделаны им во время поездки в Нидерланды, где паркетные полы встречались во многих домах.

Дюрер составлял орнаменты из правильных многоугольников, которые соединены в кольца (кольца из шести равносторонних треугольников, четырех четырехугольников, трех или шести шестиугольников, четырнадцати семиугольников, четырех восьмиугольников).

Заключение

Итак, геометрические построения - это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения.

Благодаря этой работе я познакомилась с историей возникновения циркуля, подробнее познакомилась с правилами выполнения геометрических построений, получила новые знания и применила их на практике.
Решение задач на построение циркулем и линейкой – полезное времяпровождение, позволяющее по-новому посмотреть на известные свойства геометрических фигур и их элементов. В данной работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями с помощью циркуля и линейки. Рассмотрены основные задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.
Таким образом, цель работы достигнута, поставленные задачи выполнены.

---